
Меня зовут Иван Мельников! Я – выпускник вуза НТУ «ХПИ», инженерно-физический факультет, специальность «Прикладная математика», счастливый семьянин и просто поклонник игр на удачу. С детства я увлекался лотереями. Мне всегда было интересно, по каким законам выпадают те или иные шары. С 10 лет я записываю результаты лотерей и после анализирую данные.
В моей книге «Секреты Везения или Пошаговый Алгоритм Выигрыша в Лотерее» я хочу поделиться с вами наблюдениями, накопленными годами, а также выводами, которые я смог сделать с помощью своего образования. Играйте по моей системе и уже совсем скоро вы превратите азартную игру в стабильный доход!
Математические шансы на победу
- Простой расчет с факториалами
Самыми распространенными в мире лотереями являются игры на везение типа «5 из 36» и «6 из 45». Рассчитаем шанс выигрыша в лотерее банально по теории вероятности.
Пример расчета возможности получения джекпота в лотерею «5 из 36»:
Необходимо число свободных ячеек поделить на количество возможных комбинаций. То есть первую цифру можно выбрать из 36, вторую – из 35, третью – из 34 и так далее.

Следовательно, вот формула:
Количество возможных комбинаций в лотерее типа «5 из 36» = (36*35*34*33*32) / (1*2*3*4*5) = 376 992
Шанс выигрыша составляет 1 к почти 400 000.
Давайте проделаем то же самое для лотереи типа «6 к 45».
Количество возможных комбинаций = «6 из 45» = (45*44*43*42*41*40) / (1*2*3*4*5*6) = 9 774 072.
Соответственно, шанс выигрыша составляет практически 1 к 10 млн.
- Немного о теории вероятности
Согласно давно уже известной теории у каждого шара в каждом следующем розыске есть абсолютно равный шанс выпасть по сравнению с другими.
Но не все так просто, даже согласно теории вероятности. Рассмотрим подробнее на примере подбрасывания монетки. Первый раз у нас выпал орел, тогда в следующий раз вероятность выпадения решки гораздо выше. Если орел выпал еще раз, то в следующий раз ожидаем решку с еще большей вероятностью.
С шарами, выходящими из лототронов, приблизительно та же история, но несколько сложнее и с более существенным количеством переменных. Если один шар выпал 3 раза, а другой – 10, то вероятность выпадения первого шара будет выше, чем у второго. Стоит отметить, что данный закон старательно нарушают организаторы некоторых лотерей, которые меняют лототроны время от времени. В каждом новом лототроне появляется новая последовательность.

Еще некоторые организаторы используют отдельный лототрон для каждого шара. Таким образом, необходимо рассчитывать вероятность выпадения каждого шара в каждом отдельном лототроне. Это с одной стороны немного облегчает задачу, с другой – усложняет.
Но это всего лишь теория вероятности, которая, как выяснилось, не очень-то и работает. Давайте посмотрим, какие есть секреты, основанные на сухой науке и статистических данных, накопленных за не одно десятилетие.
Почему не работает теория вероятности?
- Неидеальные условия
Первое, о чем стоит поговорить, — это калибровка лототронов. Ни один из лототронов не откалиброван идеально.

Второй нюанс – диаметры лотерейных шаров также не являются одинаковыми. Даже отличие на малейшие доли миллиметров играют роль в частоте выпадения того или иного шара.

Третья деталь – разный вес шаров. Опять же отличие может казаться вовсе не существенным, но оно также влияет на статистику, притом, значительно.

- Сумма выигрышных номеров
Если рассматривать статистику номеров, выигравших в лотерею типа «6 из 45», то можно заметить интересный факт: сумма цифр, на которые ставили игроки, колеблется между 126 и 167.
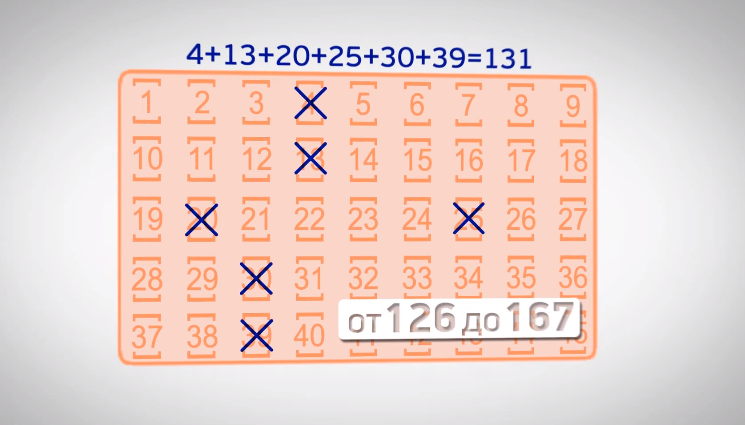
С суммой выигрышных лотерейных цифр для «5 из 36» немного другая история. Здесь выигрышные цифры составляют сумму в 83-106.
- Четные или нечетные?
Как думаете, какие цифры чаще есть в выигрышных билетах? Четные? Нечетные? Скажу вам с полной уверенностью, что в лотереях «6 из 45» этих цифр поровну.

А вот как быть с «5 из 36»? Ведь нужно выбрать всего 5 шариков, четных и нечетных не может быть равное количество. Так вот. Проанализировав результаты розыгрышей лотерей данного типа четырех последних десятилетий, могу заявить, что незначительно, но все-таки чаще, в выигрышных комбинациях появляются нечетные цифры. Особенно, те, которые содержат в себе цифру 6 или 9. Например, 19, 29, 39, 69 и так далее.
- Популярные группы чисел
Для лотереи типа «6 к 45» числа условно делим на 2 группы – от 1 до 22 и от 23 до 45. Следует отметить, что в выигрышных билетах отношение чисел, принадлежащих к группе, 2 к 4. То есть либо в билете будет 2 числа из группы от 1 до 22 и 4 числа из группы от 23 до 45 либо наоборот (4 числа из первой группы и 2 из второй).
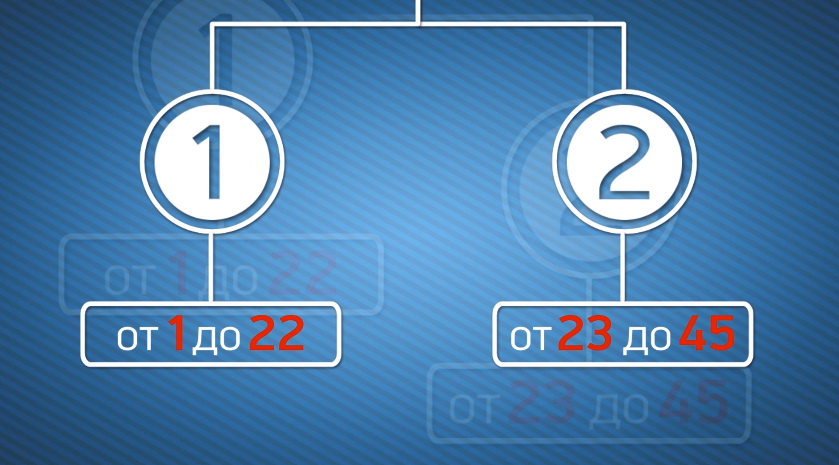
Я пришел к аналогичному выводу, анализируя статистику лотерей типа «5 из 36». Только в данном случае немного иначе дробятся группы. Давайте первой обозначим группы, в которую входят цифры от 1 до 17, а второй – ту, куда помещаются оставшиеся числа от 18 до 35. Отношение цифр из первой группы ко второй в выигрышных комбинациях в 48% случаем равно 3 к 2, а в 52% случаев – наоборот, 2 к 3.
- Стоит ли ставить на цифры из прошедших розыгрышей?
Доказано, что в 86% случаев в новом розыгрыше повторяется число, которое уже было в предыдущих розыгрышах. Поэтому просто необходимо следить за розыгрышами интересующей вас лотереи.
- Последовательные цифры. Выбирать или не выбирать?
Шанс на то, что выпадут сразу 3 последовательные цифры, очень низок, и составляет менее 0,09%. А если вы хотите поставить сразу на 5 или 6 последовательных чисел, шанса практически нет. Поэтому выбирайте разные цифры.
- Числа с единым шагом: победа или проигрыш?
Не стоит ставить на числа, которые идут в единой последовательности. Например, однозначно не нужно выбирать шаг 2 и с этим шагом делать ставку. 10, 13, 16, 19, 22 – однозначно проигрышная комбинация.

- Больше одного билета: да или нет?
Лучше играть раз в 10 недель по 10 билетам, чем раз в неделю по одному. А также играйте группами. Можно выиграть большой денежный приз и разделить его между несколькими людьми.



Статистика всемирных лотерей
- Megamillions
Одна из самых популярных в мире лотерей проводилась по следующему принципу: необходимо выбрать 5 чисел из 56, а также 1 из 46 для так называемого золотого шара.
За 5 угаданных шаров и 1 верно названный золотой счастливчик получает джекпот.
Содержание статьи

- Как рассчитать теорию вероятности в лотерее
- Самые крупные выигрыши в лотереи в истории
- Как выиграть в лотерею при помощи маятника
Теория и термины
В мире постоянно проводится множество лотерей с самыми различными правилами, условиями победы, призами, однако существуют общие принципы расчета вероятности выигрыша, которые можно адаптировать под условия той или иной конкретной лотереи. Но для начала желательно определиться с терминологией.
Итак, вероятность – это вычисленная оценка возможности того, что произойдет определенное событие, которая чаще всего выражается в форме отношения числа желаемых событий к общему числу исходов. Например, вероятность выпадения «орла» при подбрасывании монетки – один к двум.
Исходя из этого, очевидно, что вероятность выигрыша – это соотношение количества выигрышных комбинаций к числу всех возможных. Однако нельзя забывать, что критерии и определения понятия «выигрыш» тоже могут быть разными. К примеру, в большинстве лотерей используется такое определение как «класс выигрыша». Требования к выигрышу третьего класса ниже, чем к выигрышу первого, поэтому вероятность выигрыша первого класса самая низкая. Как правило, таким выигрышем является джек-пот.
Еще один значимый момент в расчетах заключается в том, что вероятность двух связанных событий вычисляется путем перемножения вероятностей каждого из них. Проще говоря, если вы подбросите монетку два раза, то вероятность выпадения «орла» каждый раз будет равна один к двум, но шанс, что «орел» выпадет оба раза, составит лишь один к четырем. В случае с тремя подбрасываниями шанс вообще упадет до одного к восьми.
Расчет шансов
Таким образом, для расчета шанса выигрыша джек-пота в абстрактной лотерее, где нужно верно угадать несколько выпавших значений из определенного числа шаров (например, 6 из 36), нужно рассчитать вероятность выпадения каждого из шести шаров и перемножить их между собой. Учтите, что с уменьшением числа шаров, оставшихся в барабане, вероятность выпадения нужного шара меняется. Если для первого шара вероятность того, что выпадет нужный, равна 6 к 36, то есть, 1 к 6, то для второго шанс составит 5 к 35 и так далее. В данном примере вероятность того, что билет окажется выигрышным составит 6x5x4x3x2x1 к 36x35x34x33x32x31, то есть 720 к 1402410240, что будет равно 1 к 1947792.
Несмотря на такие пугающие числа, люди регулярно выигрывают в лотереи по всему миру. Не забывайте, что даже если вы не возьмете главный приз, существуют еще выигрыши второго и третьего классов, вероятность получить которые намного выше. Кроме того, очевидно, что наилучшей стратегией является покупка нескольких билетов одного тиража, так как каждый дополнительный билет кратно увеличивает ваши шансы. Например, если купить не один билет, а два, то и вероятность победы будет в два раза больше: два из 1,95 миллиона, то есть примерно 1 к 950 тысячам.
Вероятность или шанс угадать комбинацию, развёрнутую ставку, группу чисел —
в зависимости от количества выбранных номеров, для лотерей 5 из 36, 6 из 45, 7 из 49, 6 из 49, 4 из 20, Рапидо —
смотрим по этой ссылке
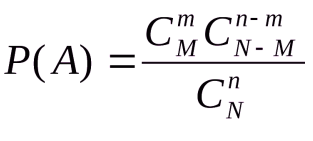
Вероятности в популярных лотереях
5 из 36, 6 из 45, 7 из 49, 6 из 36, 4 из 20, Матчбол, Рапидо

На этом графике хорошо видно количество комбинаций. Чем меньше сектора,
тем вероятней джек пот, на одну простую комбинацию.
В лотереях 5 из 36 и Рапидо самое малое количество комбинаций — практически не видно на фоне остальных. Если учитывать призовой фонд, то в лотереях Рапидо, 4 из 20, — он самый большой (67% призового фонда), следовательно, выигрыши в низших категория будут чаще, если это можно назвать «выигрышем»… — на дистанции «слив» всё равно обеспечен, если, конечно, не «словится» суперприз! Тем не менее, чем больше возврат при длительной игре, тем больше можно ставить комбинаций, тем вероятней суперприз.
По вероятности выиграть суперприз, лотерея 5 из 36 считается лучшей из всех (без дополнительного), — сейчас «приз», который может достигать десятков миллионов. Далее по популярности у игроков следует лотерея 6 из 45, в которой шансы 1 на 8 миллионов комбинаций.
Лотерея 6 из 45 отличается ещё от остальных неплохой выплатой за приз второй категории, по такому параметру (вероятность-выплата)
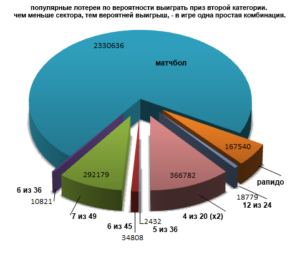
Сравним популярные лотереи по вероятности выиграть приз второй категории.
Чем меньше сектора, тем вероятней выигрыш, — в игре одна простая комбинация.
При выборе лотереи желательно учитывать потенциальную выплату за приз второй категории, угадать который более реально. Для этого нужно просмотреть выплаты на сайте лотерей. Вероятность второй категории лучше не превышать 1: 100 000. В этом плане, например, лотереи 7 из 49 и 4 из 20 выглядят не очень привлекательно, у них вероятность второй категории практически сравнима с первой категорией приза лотереи 5 из 36 (1: 376 992). В какую лотерею играть, решает каждый сам!

